En este post se explica qué es la regla Sturges y cuál es su fórmula. También encontrarás un ejemplo resuelto paso a paso de la regla de Sturges y, además, una calculadora online de la regla de Sturges.
Índice
¿Cuál es la regla de Sturges?
La regla de Sturges es una regla que sirve para calcular el número clases o intervalos idóneo en los que se debe dividir un conjunto de datos.
La fórmula de la regla de Sturges establece que el número de clases es igual a uno más el logaritmo en base dos del número total de datos.
Donde 
es el número de clases o intervalos y 
es el número total de observaciones de la muestra.
La mayoría de calculadoras solo permiten hacer cálculos con logaritmos de base 10. En tal caso, puedes utilizar esta fórmula equivalente:
La regla de Sturges fue creada en 1926 por el estadístico alemán Herbert Sturges.
Ejemplo de la regla de Sturges
Ahora que ya sabemos en qué consiste la regla de Sturges, vamos a ver resolviendo un ejercicio paso a paso cómo se calculan en estadística los intervalos de un conjunto de datos mediante la regla de Sturges.
- Se ha medido la altura a una muestra de 50 personas diferentes y se han registrado todos los valores en la siguiente tabla de datos. Aplica la regla de Sturges para dividir el conjunto de datos en intervalos y luego representa los datos en un histograma.
En primer lugar, tenemos que separar los datos en intervalos. En total hay 50 datos, por lo tanto, usamos la regla de Sturges con este valor:
![\begin{array}{l}c=1+\log_2(N)\\[2ex]c=1+\log_2(50)\\[2ex]c=1+5,64\\[2ex]c=6,64\\[2ex]c\approx 7\end{array}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-40eb7a41a4b3ea431426c36cfe32a810_l3.svg "Rendered by QuickLaTeX.com")
De modo que debemos separar los datos y agruparlos en siete intervalos. Ahora necesitamos saber la amplitud de cada intervalo, para ello, simplemente tenemos que dividir el valor máximo menos el valor mínimo entre el número total de intervalos:
En definitiva, tienen que haber 7 intervalos con una amplitud de 9, así que los intervalos calculados mediante el método de Sturges son:
Una vez hemos calculado los intervalos, tenemos que contar el número de veces que aparece un dato en cada intervalo y construir la tabla de frecuencias:
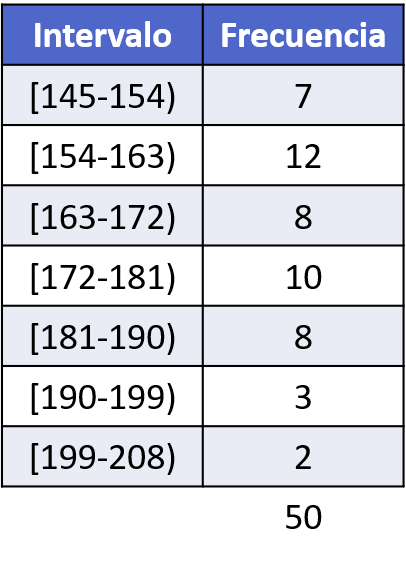
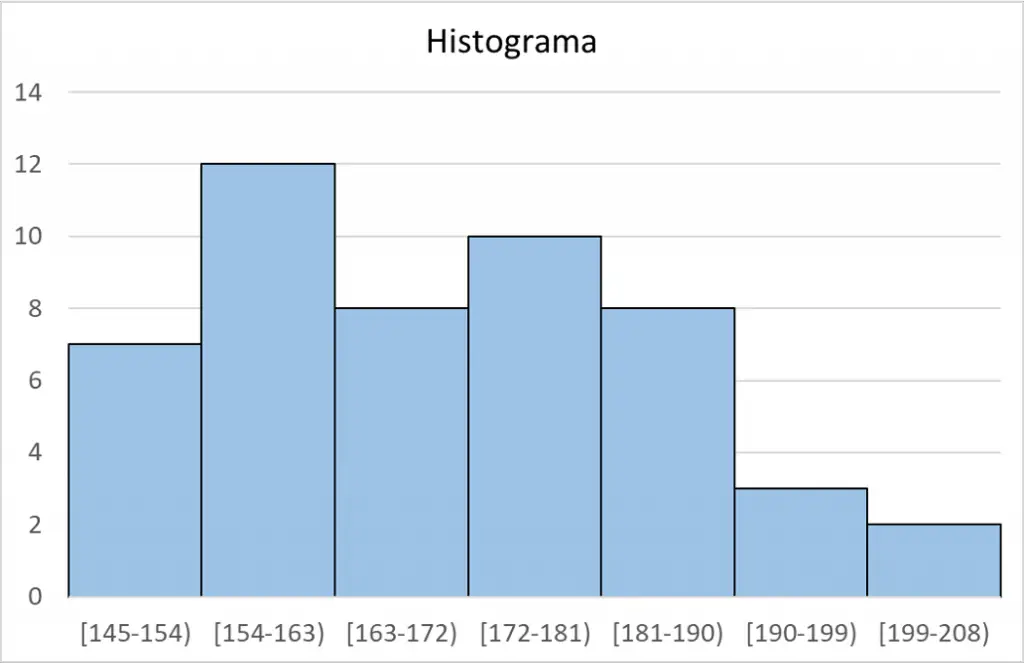
Finalmente, a partir de la tabla de frecuencias podemos hacer el histograma para representar los datos gráficamente:
Calculadora de la regla de Sturges
Introduce el número total de datos de la muestra y haz clic en «Calcular», seguidamente la calculadora devolverá el número de intervalos calculado según la regla de Sturges.
Asi no parece tan complicado. Pero donde puedo encontrar la tabla logaritmica para ver el log2 de 50?
Hola Felipe,
Para calcular el logaritmo en base 2 de cualquier número puedes utilizar una calculadora. En caso de que tu calculadora solo pueda hacer cálculos con logaritmos en base 10, puedes aplicar la siguiente fórmula:
Excelente la explicación.
Gracias
¡Gracias a ti Griceldo!
Gracias por esa explicación fácil de comprender pero ni en clase lo vi tan fácil como en este blog felicidades
¡Muchísimas gracias Cindy!
Cuando se construyen las clases o intervalos según esta regla, los límites de cada clase no son mutuamente excluyentes, como defino dónde debo colocar un valor que coincida con el extremo?por ejemplo; si alguna persona tuviera una altura de 154 en cual clase la ubico en la primera o segunda?
Hola Yoleia,
Si el límite de un intervalo tiene un corchete [ ] a su lado, significa que es número se incluye en el límite. Por otro lado, si el límite del intervalo tiene un paréntesis ( ) a su lado, quiere decir que dicho límite no está incluido en el intervalo.
Por lo tanto, el valor 154 se encuentra dentro del intervalo [154,163) y está fuera del intervalo [145,154).
Feliz noche de dnd sale el número 5,64?
Es el resultado del logaritmo en base 2 de 50 🙂
Muy buena y clara la explicación, saludos.
¡Gracias Reyes!
Entendí muchas cosas aquí, gracias por todo.
¡Estupendo Angel! ¡Gracias a ti por el comentario!