▷ Ecuación de regresión

En este post se explica qué es una ecuación de regresión y para qué sirve. Asimismo, encontrarás cómo hallar una ecuación de regresión, un ejercicio resuelto y, por último, una calculadora online para calcular la ecuación de regresión de cualquier conjunto de datos.

Índice

¿Cuál es la ecuación de regresión?

La ecuación de regresión es aquella ecuación que mejor se ajusta a una gráfica de puntos, es decir, la ecuación de regresión es la mejor aproximación de un conjunto de datos.

La ecuación de regresión es de la forma y=β₀+β₁x, donde β₀ es la constante de la ecuación y β₁ es la pendiente de la ecuación.

$y=\beta_0+\beta_1x$

Si te fijas en la ecuación de regresión, se trata de la ecuación de una recta. Esto significa que la relación entre la variable independiente X y la variable dependiente Y se modela como una relación lineal, ya que la recta representa una relación lineal.

Así pues, la ecuación de regresión nos permite relacionar matemáticamente la variable independiente y la variable dependiente de un conjunto de datos. Aunque generalmente la ecuación de regresión no es capaz de determinar con exactitud el valor de cada observación, sí que sirve para obtener una aproximación de su valor.

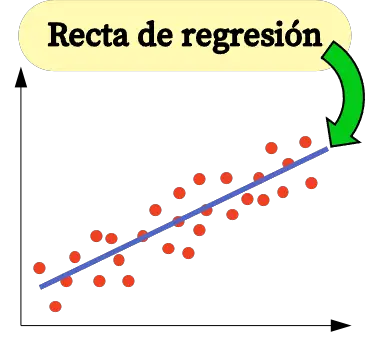
Como puedes ver en la gráfica anterior, la ecuación de regresión nos ayuda a ver la tendencia de un conjunto de datos y qué tipo de relación hay entre la variable independiente y la variable dependiente.

Cómo calcular la ecuación de regresión

Las fórmulas para calcular los coeficientes de la ecuación de regresión lineal simple son las siguientes:

$\begin{array}{c}\beta_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[12ex]\beta_0=\overline{y}-\beta_1\overline{x}\end{array}$

Donde:

$\beta_0$ es la constante de la ecuación de regresión.
$\beta_1$ es la pendiente de la ecuación de regresión.
$x_i$ es el valor de la variable independiente X del dato i.
$y_i$ es el valor de la variable dependiente Y del dato i.
$\overline{x}$ es la media de los valores de la variable independiente X.
$\overline{y}$ es la media de los valores de la variable dependiente Y.

Ejemplo del cálculo de la ecuación de regresión

Después de realizar un examen de estadística, se ha preguntado a cinco estudiantes cuántas horas de estudio dedicaron al examen, los datos se muestran en la tabla de abajo. Calcula la ecuación de regresión de los datos estadísticos recopilados para relacionar linealmente las horas de estudio con la nota obtenida. Luego, determina qué nota sacará un alumno que haya estudiado 8 horas.

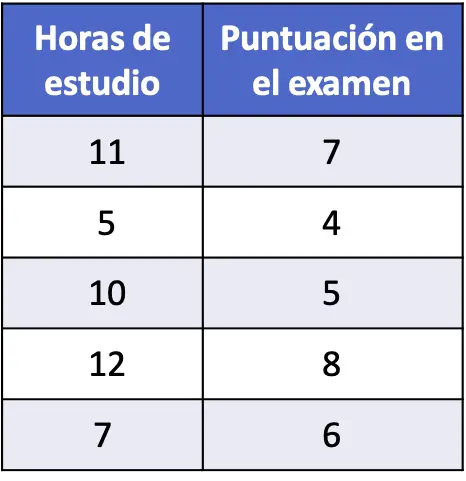
Para hallar la ecuación de regresión de la muestra de datos tenemos que determinar los coeficientes b₀ y b₁ de la ecuación y, para ello, tenemos que utilizar las fórmulas vistas en el apartado de arriba.

No obstante, para poder aplicar las fórmulas de la ecuación de regresión lineal primero tenemos que calcular la media de la variable independiente y la media de la variable dependiente:

$\begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}$

Ahora que ya sabemos las medias de las variables, calculamos el coeficiente β₁ del modelo usando su fórmula correspondiente:

$\begin{array}{c}\beta_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] \beta_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]\beta_1=0,4412\end{array}$

Por último, calculamos el coeficiente β₀ del modelo empleando su fórmula correspondiente:

$\begin{array}{l}\beta_0=\overline{y}-\beta_1\overline{x}\\[3ex]\beta_0=6-0,4412\cdot 9 \\[3ex]\beta_0=2,0294\end{array}$

En definitiva, la ecuación de la recta de regresión lineal del problema es la siguiente:

$y=2,0294+0,4412x$

A continuación puedes ver la representación gráfica de la muestra de datos junto con la ecuación del modelo de regresión lineal simple:

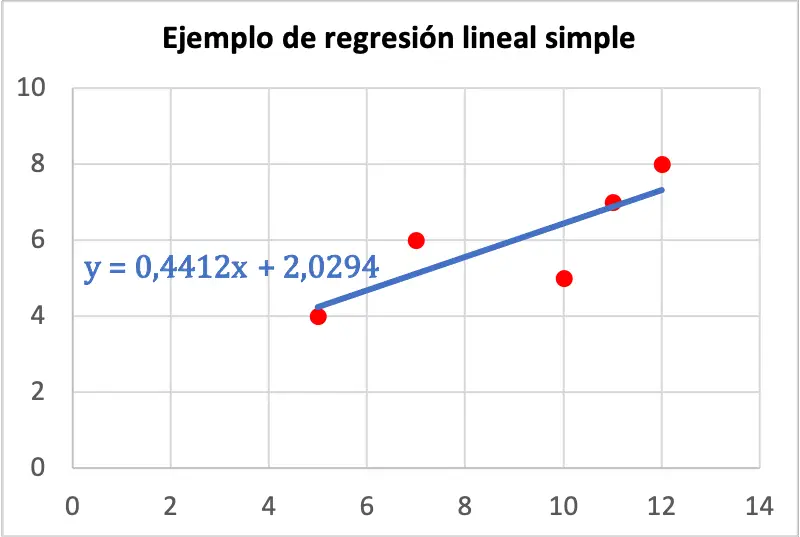
Una vez hemos calculado la ecuación de regresión, para hacer una predicción de la nota que conseguirá un alumno que ha estudiado 8 horas simplemente tenemos que sustituir dicho valor en la ecuación de regresión obtenida:

$y=2,0294+0,4412\cdot 8=5,56$

Así pues, según el modelo de regresión lineal realizado, si un alumno ha estudiado ocho horas, obtendrá una puntuación de 5,56 en el examen.

Calculadora de la ecuación de regresión

Introduce una muestra de datos en la siguiente calculadora para calcular su ecuación de regresión. Debes separar las parejas de datos, de manera que en el primer recuadro solo haya los valores de la variable independiente X y en el segundo recuadro únicamente estén los valores de la variable dependiente Y.

Los datos deben separase por un espacio e introducirse usando el punto como separador decimal.

Ecuación de regresión lineal múltiple

Acabamos de ver cuál es la ecuación de regresión lineal simple, no obstante, el modelo de regresión también puede ser un modelo de regresión lineal múltiple, el cual incluye dos o más variables independientes. De manera que la regresión lineal múltiple permite relacionar varias variables explicativas con una variable respuesta de manera lineal.

La ecuación del modelo de regresión lineal múltiple es la siguiente:

$y=\beta_0+\beta_1 x_1+\beta_2 x_2+\dots+\beta_m x_m+\varepsilon$

Donde:

$y$ es la variable dependiente.
$x_i$ es la variable independiente i.
$\beta_0$ es la constante de la ecuación de la regresión lineal múltiple.
$\beta_i$ es el coeficiente de regresión asociado a la variable $x_i$ .
$\bm{\varepsilon}$ es el error o residuo, es decir, la diferencia entre el valor observado y el valor estimado por el modelo.
$m$ es el número total de variables del modelo.

De modo que si tenemos una muestra con un total de $n$ observaciones, podemos plantear el modelo de regresión lineal múltiple en forma matricial:

$\begin{pmatrix}y_1\\y_2\\\vdots\\y_n\end{pmatrix}=\begin{pmatrix}1&x_{11}&\dots&x_{1m}\\1&x_{21}&\dots&x_{2m}\\ \vdots&\vdots&\ddots&\vdots\\1&x_{n1}&\dots&x_{nm}\end{pmatrix}\cdot\begin{pmatrix}\beta_0\\\beta_1\\\vdots\\\beta_m\end{pmatrix}+\begin{pmatrix}\varepsilon_1\\\varepsilon_2\\\vdots\\\varepsilon_n\end{pmatrix}$

La expresión matricial anterior se puede reescribir asignando una letra a cada matriz:

$Y=X\beta+\varepsilon$

Así pues, aplicando el criterio de los mínimos cuadrados, se puede llegar a la fórmula para estimar los coeficientes de una ecuación de regresión lineal múltiple:

$\widehat{\beta}=\left(X^tX\right)^{-1}X^tY$

No obstante, aplicar esta fórmula es muy laborioso y lleva mucho tiempo, por lo que en la práctica se recomienda usar un software informático (como Minitab o Excel) que permite realizar un modelo de regresión múltiple de manera mucho más rápida.

➤ Ver: ¿Qué es la regresión lineal múltiple?

¿Cuál es la ecuación de regresión?

Cómo calcular la ecuación de regresión

Ejemplo del cálculo de la ecuación de regresión

Calculadora de la ecuación de regresión

Ecuación de regresión lineal múltiple

Deja un comentario Cancelar respuesta