En este post se explica qué son las distribuciones bidimensionales en estadística. También encontrarás un ejemplo de una distribución bidimensional y varias fórmulas que nos permiten estudiar este tipo de distribuciones.
Índice
¿Qué es una distribución bidimensional?
Una distribución bidimensional es aquella en la que cada elemento le corresponden los valores de dos variables. Es decir, en lugar de tener un único valor, en una distribución bidimensional cada individuo tiene un par de valores (xi, yi).
Por ejemplo, si analizamos las notas que han obtenido los alumnos de una clase en matemáticas y estadística, a cada alumno le corresponden dos notas, por lo que se trata de una distribución bidimensional.
La parte de la estadística que se encara de estudiar las distribuciones bidimensionales es la estadística bidimensional.
Ejemplo de distribución bidimensional
Una vez hemos visto la definición de distribución bidimensional, vamos a ver un ejemplo de este tipo de distribuciones para entender mejor el concepto.
- En la siguiente tabla de doble entrada se han recogido las notas de matemáticas y estadística de una muestra de 20 alumnos. Representa el conjunto de datos en un gráfico y analízalo.
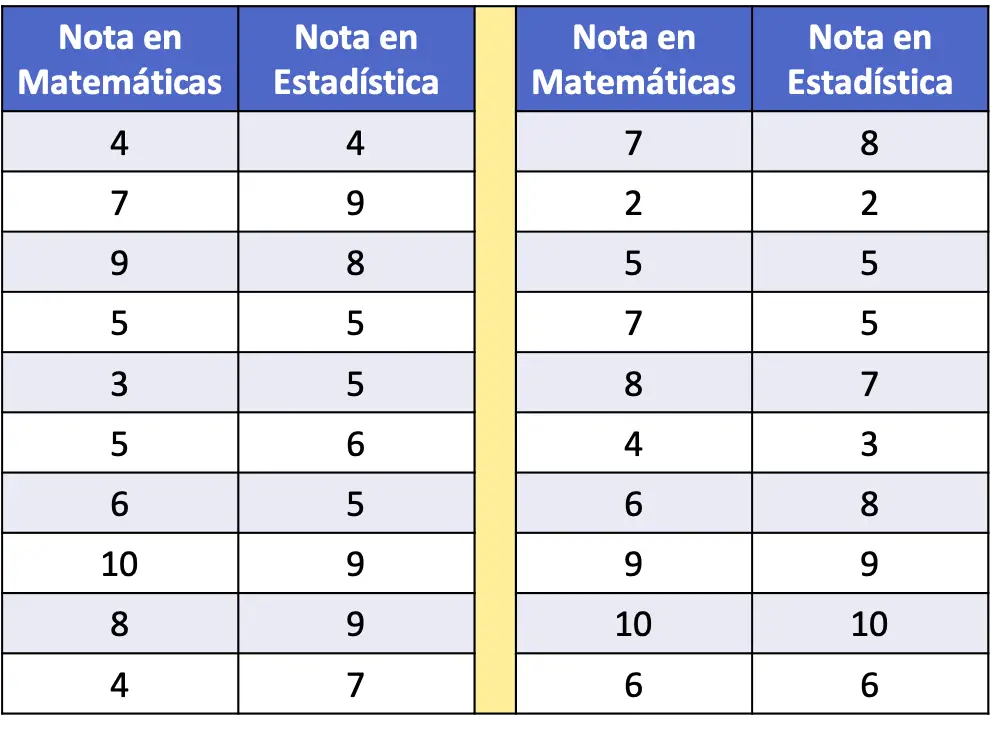
Para representar los datos de la distribución bidimensional en un gráfico simplemente debemos dibujar dos ejes, calibrarlos y representar un punto en la gráfica por cada pareja de datos. Recuerda que un punto en una gráfica se pone donde se cortan las rectas imaginarias correspondientes a cada uno de sus valores.
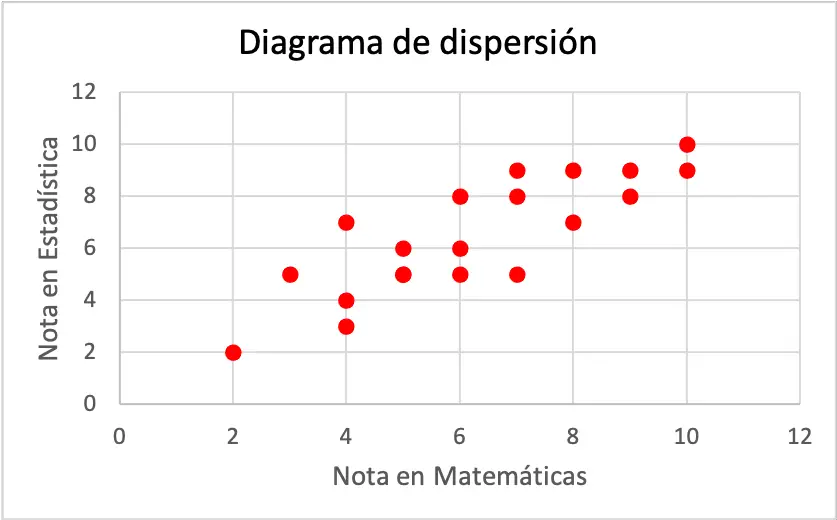
Cada eje del diagrama representa una variable, en concreto, el eje horizontal pertenece a la nota conseguida en matemáticas y, por otro lado, el eje vertical corresponde a la nota obtenida en estadística.
Como puedes ver en el gráfico de dispersión, las dos variables tienen una correlación positiva, ya que una variable aumenta a medida que la otra variable también aumenta. Por lo tanto, se concluye que si un alumno consigue mejor nota en matemáticas es más probable que también saque mejor nota en estadística, y al revés.
Sin embargo, la conclusión anterior no significa que una variable sea la causa de la otra, ya que obtener una buena nota en matemáticas no te garantiza automáticamente conseguir una buena nota en estadística sin hacer nada, sino que se deben estudiar las dos asignaturas.
Fórmulas de distribuciones bidimensionales
A continuación veremos varias fórmulas que sirven para analizar series de datos de distribuciones bidimensionales.
Covarianza
En estadística, la covarianza es un valor que indica el grado de variación conjunta de dos variables aleatorias. De modo que covarianza sirve para analizar la dependencia entre las dos variables de la distribución bidimensional.
Lla fórmula para calcular la covarianza entre dos variables es la siguiente:

Correlación
La correlación es una medida estadística que indica el grado de relación entre dos variables. En concreto, la correlación lineal sirve para determinar cuánto de correlacionadas linealmente están dos variables distintas.
Dos variables están relacionadas cuando al variar los valores de una variable también cambian los valores de la otra variable. Por ejemplo, si al aumentar la variable A también aumenta la variable B, existe una correlación entre las variables A y B.
El coeficiente de correlación es el valor de la correlación entre dos variables. La fórmula para calcularlo es la siguiente:

El coeficiente de correlación se usa para analizar la relación entre las dos variables que componen la distribución bidimensional.
Recta de regresión
La recta de regresión es la recta que mejor se ajusta a una nube de puntos y que, por tanto, mejor describe un conjunto de datos formado por dos variables. Es decir, la recta de regresión sirve para determinar un modelo que describe una determinada distribución bidimensional.
Así pues, la ecuación de la recta de regresión relaciona matemáticamente las dos variables de una distribución bidimensional. Aunque generalmente la recta de regresión no es capaz de determinar con exactitud el valor de cada observación, sí que nos permite obtener una aproximación de su valor.
Como puedes ver en la gráfica anterior, la recta de regresión nos ayuda a ver la tendencia de un conjunto de datos, además, es útil para predecir el valor de las variables.
